 |
| Imatge proporcionada per la base de dades manuscrita MNIST |
En aquest cas, sorgeixen dificultats per diferenciar zeros de sisos. Es podria establir algun tipus de tall, però, com decidir el tall en primer lloc?. Com es pot veure, es fa bastant complicat compilar una llista heurística (és a dir, regles i conjectures) que classifiquen amb precisió els dígits manuscrits. I hi ha tantes classes de més problemes que entren en aquesta categoria. Reconèixer objectes, comprendre conceptes, comprendre el discurs. No se sap quin programa escriure, perquè encara no se sap com ho fan els nostres propis cervells. I fins i tot si es tenia una bona idea sobre com fer-ho, el programa podria ser horriblement complicat.
Així que, en comptes d'intentar escriure un programa, s'intenta desenvolupar un algoritme que un ordinador pugui utilitzar per mirar centenars o milers d'exemples (i les respectives respostes correctes), i després l'ordinador utilitza aquesta experiència per resoldre el mateix problema en situacions noves. Essencialment, l'objectiu és ensenyar a l'ordinador a resoldre, per exemple, d'una manera molt similar a com es pot ensenyar a un nen petit a distingir un gat d'un gos.
Durant les últimes dècades, els científics informàtics han desenvolupat una sèrie d'algorismes que intenten permetre que els ordinadors aprenguin a resoldre problemes a través d'exemples. L'aprenentatge profund, que va ser teoritzat per primera vegada a principis dels 80 (i potser fins i tot abans), és un paradigma per a la realització de l'aprenentatge automàtic. I a causa d'una sèrie d'investigacions modernes, l'aprenentatge profund torna a augmentar, ja que s'ha demostrat que és bastant bo per ensenyar a les computadores a fer el que el nostre cervell pot fer de forma natural.
Un dels grans reptes amb els models tradicionals d'aprenentatge automàtic és un procés anomenat extracció de característiques. Concretament, el programador necessita informar a l'ordinador quins tipus de coses hauria de buscar, serà informatiu en la presa de decisions. L'alimentació de l'algorisme de dades en brut rares vegades funciona, de manera que l'extracció de característiques és una part crítica del flux de treball tradicional de l'aprenentatge de màquina. Això suposa una gran càrrega per al programador, i l'eficàcia de l'algoritme es basa en gran mesura en què és el programador més atractiu. Per a problemes complexos com el reconeixement d'objectes o el reconeixement d'escriptura manual, aquest és un repte enorme.
L'aprenentatge profund és un dels únics mètodes pels quals podem evitar els reptes de l'extracció de funcions. Això és degut a que els models d'aprenentatge profund són capaços d'aprendre a centrar-se en les característiques correctes per si mateixos, que requereixen poca orientació del programador. Això fa que l'aprenentatge profund sigui una eina extremadament poderosa per a l'aprenentatge automàtic modern.
Una primera mirada a xarxes neuronals
L'aprenentatge profund és una forma d'aprenentatge automàtic que utilitza un model de computació molt inspirat en l'estructura del cervell. Per això, s'anomena aquest model una xarxa neuronal. La unitat bàsica fonamental d'una xarxa neuronal és la neurona, que en realitat és, conceptualment, bastant simple.
Cada neurona té un conjunt d'entrades, cadascuna d'elles té un pes específic. La neurona calcula alguna funció en aquestes entrades ponderades. Una neurona lineal pren una combinació lineal de les entrades ponderades. Una neurona sigmoidea fa alguna cosa una mica més complicada:
Alimenta la suma ponderada de les entrades a la funció logística. La funció logística retorna un valor entre 0 i 1. Quan la suma ponderada és molt negativa, el valor retornat és molt proper a 0. Quan la suma ponderada és molt gran i positiva, el valor retornat és molt proper a 1. Per a més matemàticament inclinat, la funció logística és una bona elecció perquè té una bonica derivació, que fa que l'aprenentatge sigui un procés més senzill. Però a banda de les dades tècniques, independentment de la funció que utilitzi la neurona, el valor que calcula es transmet a altres neurones com a sortida. A la pràctica, les neurones sigmoides s'utilitzen molt més sovint que les neurones lineals, ja que permeten algorismes d'aprenentatge molt més versàtils en comparació amb les neurones lineals.
Una xarxa neuronal es produeix quan comencem a connectar les neurones entre elles, a les dades d'entrada i als punts de venda, que corresponen a la resposta de la xarxa al problema de l'aprenentatge. Per facilitar la visualització d'aquesta estructura, he inclòs un exemple senzill d'una xarxa neuronal a continuació. Deixem que w(k) i, j sigui el pes de l'enllaç que uneix la neurona ith a la kth capa amb la jth neurona a la capa k + 1 st:
De manera similar a com les neurones generalment s'organitzen en capes del cervell humà, les neurones de les xarxes neuronals també s'organitzen en capes, on les de la capa inferior reben senyals de les entrades; on les de les capes superiors tenen les seves connexions connectades amb la resposta i on normalment no hi ha connexions entre neurones en la mateixa capa (tot i que aquesta és una restricció opcional, les connectivitats més complexes requereixen més anàlisi matemàtica). També s'observen que, en aquest exemple, no hi ha connexions que condueixen des d'una neurona en una capa superior a una neurona en una capa inferior (és a dir, sense cicles dirigits). Aquestes xarxes neuronals s'anomenen xarxes neuronals avançades en comparació amb les seves contraparts, que es diuen recursives xarxes neuronals (de nou són molt més complicades d'analitzar i entrenar). Per fer-ho més fàcil, només ens centrem en les xarxes avançades al llarg d'aquesta discussió. Seguidament us oferim un conjunt d'algunes notes més importants per tenir en compte:
- Encara que totes les capes tenen el mateix nombre de neurones en aquest exemple, no és necessari.
- No es requereix que una neurona tingui la seva sortida connectada a les entrades de cada neurona en la següent capa. De fet, seleccionant quines neurones es connecten a quines altres neurones de la capa següent és un art que prové de l'experiència. Permetre la connectivitat màxima amb més freqüència no resultarà en un excedent, un concepte que més endavant discutirem.
- Les entrades i sortides són representacions vectoritzades. Per exemple, es pot imaginar una xarxa neuronal on les entrades són els valors dels píxels RGB individuals en una imatge representada com a vector. L'última capa pot tenir dues neurones que corresponen a la resposta al nostre problema: [0,1] si la imatge conté un gos, [1,0] si la imatge conté un gat, [0,0] si no conté cap dels dos, i [1,1] si els conté a tots dos.
- Les capes de neurones que es troben intercalades entre la primera capa (capa d'entrada) i l'última capa de neurones (capa de sortida), s'anomenen capes ocultes. Això és perquè aquí és on la major part de la màgia està passant quan la xarxa neuronal intenta resoldre problemes. Fer una ullada a les activitats de les capes amagades pot dir-vos molt sobre les funcions que la xarxa ha après a l'extreure de les dades.
Formar una neurona individual
Les coses comencen a posar-se interessants, però encara falta un gran tros de la imatge. Se sap com una xarxa neuronal pot calcular les respostes de les entrades, però s'ha assumit que sap quins pesos utilitzar per començar. Esbrinar quins pesos ha de ser la part més difícil del problema, i això es fa mitjançant un procés anomenat entrenament. Durant l'entrenament, es mostren a la xarxa neuronal una gran quantitat d'exemples de formació i es modifiquen de forma iterativa els pesos per minimitzar els errors que fem sobre els exemples de formació.
Començar amb un exemple senzill que implica una única neurona lineal per motivar el procés. Cada dia es menja al menjador on el menjar està format per hamburgueses, patates fregides i refrescos. Es compren un nombre de porcions de cada element. Es vol poder predir quant costarà el menjar, però no es coneixen els preus de cada element individual. L'únic que dirà el caixer és el preu total del menjar.
Com es pot solucionar aquest problema? Bé, Es podria començar per ser intel·ligents per escollir els casos de formació. Per a un dinar es podria comprar només una sola porció d'hamburgueses, per a un altre només es podria comprar una sola porció de patates fregides, i després per al nostre últim sopar es podria comprar una sola porció de refresc. En general, triar casos de formació intel·ligent és una bona idea. Hi ha molta investigació que demostra que mitjançant l'enginyeria d'un conjunt de formació intel·ligent, es podria aconseguir que la xarxa neuronal sigui molt més eficaç. El problema amb aquest enfocament és que en situacions reals, això rarament obté un 10% del l'èxit del resultat. Per exemple, quin és l'anàleg d'aquesta estratègia en el reconeixement d'imatges?
Suposant que es te un munt d'exemples de formació, a continuació es pot calcular el que la xarxa neuronal generarà en l'exemple d'entrenament ith utilitzant la fórmula simple del diagrama. Es vol entrenar la neurona perquè es puguin triar els pesos òptims possibles: els pesos que minimitzen els errors que es fan sobre els exemples de formació. En aquest cas, diguem que es vol minimitzar l'error quadrat sobre tots els exemples d'entrenament que es trobaran. Més formalment, si se sap que t(i) és la resposta veritable per al i-èsim exemple d'entrenament e i(i) és el valor calculat per la xarxa neuronal, volem minimitzar el valor de la funció d'error E:
Ara, en aquest moment, es podria estar pensant, esperant ... Per què molestar-se amb aquesta funció d'error sense sentit quan es tenen un munt de variables (pesos) i es te un conjunt d'equacions (una per a cada exemple de formació)? No es podria solucionar aquest problema configurant un sistema lineal d'equacions? Això donaria automàticament un error de zero assumint que es te un conjunt consistent d'exemples de formació. Aquesta és una observació intel·ligent, però la perspicàcia, malauradament, no generalitza bé. Recordar que, tot i que s'està utilitzant una neurona lineal aquí, aquestes, no s'utilitzen gaire a la pràctica, ja que es limiten al que poden aprendre. Per tant, ara es el moment de començar a utilitzar neurones no lineals com les neurones sigmoides comentades abans.
Per tant, potser es pot utilitzar un enfocament iteratiu que generalitzi en exemples no lineals. S'intenta visualitzar com es podria minimitzar l'error quadrat en tots els exemples d'entrenament simplificant el problema. Diguem que s'està tractant amb una neurona lineal amb només dues entrades (i, per tant, només dos pesos, w1 i w2). A continuació, es pot imaginar un espai tridimensional on les dimensions horitzontals corresponen als pesos w1 i w2, i hi ha una dimensió vertical que correspon al valor de la funció d'error E. Així, en aquest espai, els punts del pla horitzontal corresponen a la configuració diferent dels pesos i l'alçada en aquests punts corresponen a l'error en què estem incorrent, sumats en tots els casos de formació. Si es tenen en compte els errors que es fan sobre tots els pesos possibles, s'obté una superfície en aquest espai tridimensional.
També podem visualitzar convenientment aquesta superfície com un conjunt de contorns el·líptics, on l'error mínim es troba al centre de les el·lipsis:
Així doncs, diguem que s'està en algun lloc del pla horitzontal (escollint una inicialització aleatòria per als pesos). Com aconseguir el punt en el plànol horitzontal amb el menor valor d'error? Una estratègia és moure sempre de manera perpendicular a les línies de contorn. Per exemple, a la ruta indicada per les fletxes vermelles. Molt clar, es pot veure que, seguint aquesta estratègia, s'arribarà al punt d'error mínim. El que és particularment interessant és que moure's perpendicularment a les línies de contorn equival a prendre el camí del descens més pronunciat per la tassa parabòlica.
Aquest és un resultat bastant sorprenent del càlcul, i ens dóna el nom d'aquesta estratègia general per a la formació de xarxes neuronals: descens de gradient.
Tarifes d'aprenentatge i la regla del Delta
En la pràctica, a cada pas de moure's perpendicularment al contorn, s'ha de determinar fins a quin punt es vol caminar abans de tornar a calcular la nova adreça. Aquesta distància ha de dependre de la inclinació de la superfície. Per què? Com més a prop al mínim, més curts cal avançar. Sabent que s'està a prop del mínim, perquè la superfície és molt més plana, per la qual cosa es pot utilitzar la inclinació com a indicador de la proximitat que tenim al mínim. Es multiplica aquesta mesura d'inclinació amb un factor constant predeterminat ε, la taxa d'aprenentatge. Escollir la taxa d'aprenentatge és un problema difícil. Si es tria una taxa d'aprenentatge que és massa petita, hi ha el risc a prendre massa temps durant el procés de formació. Si es tria una taxa d'aprenentatge massa gran, probablement es començarà a divergir del mínim (això és bastant fàcil de visualitzar). Els algorismes d'entrenament moderns adapten la taxa d'aprenentatge per superar aquest difícil repte.
Posar totes les peces, es coneix com la regla delta per formar la neurona lineal. La regla delta estableix que donada una velocitat d'aprenentatge ε, cal canviar el pes wk en cada iteració de la formació de Δwk = Σiεxk (t (i) -y (i)). Derivar aquesta fórmula es deixa com un exercici per al lector experimentat.
Malauradament, simplement prenent el camí del descens més pronunciat, no sempre resol quan tenim neurones no lineals. La superfície d'error pot arribar a ser complicada i podria haver-hi un mínim local múltiple. Com a resultat, l'ús d'aquest procediment podria arribar a un mínim local que no és el mínim global. Com a resultat, en la pràctica, la formació de xarxes neuronals implica una modificació del descens de degradat anomenat descens gradient estocàstic, que intenta utilitzar l'aleatorització i el soroll per trobar el mínim global amb una alta probabilitat en una superfície d'error complexa. Passant a la neurona sigmoidea.
Aquesta secció i la següent es tornaran una mica pesades amb les matemàtiques, així que acaba de ser previngut. Si no us trobeu còmode amb el càlcul multivariant, no dubti a saltar-los i passar a les seccions restants. En cas contrari, anem a submergir-hi bé!
Recordant el mecanisme pel qual les neurones logístiques computen el valor de sortida de les seves entrades:
A més, sorprenentment, la derivada de la sortida respecte al logit és bastant simple si s'expressa en termes de sortida.
Llavors usant la regla de la cadena per obtenir la derivada de la sortida respecte a cada pes:
Posant tot això junt, ara es pot calcular la derivada de la funció d'error respecte a cada pes:
Per tant, la regla final per a la modificació dels pesos es converteix en:
Com es pot observar, la nova regla de modificació és igual que la delta, excepte amb els termes multiplicatius addicionals inclosos per explicar el component logístic de la neurona sigmoidea.
L'algoritme de backpropagation
Ara estem preparats per abordar el problema de la formació de xarxes neuronals multicapa (en lloc de només neurones individuals). Quina és la idea? No se sap què haurien de fer les unitats ocultes, però el que es pot fer és calcular la rapidesa amb que l'error canvia a mesura que es canvia una activitat oculta. Essencialment intentant trobar el camí del descens més fort.
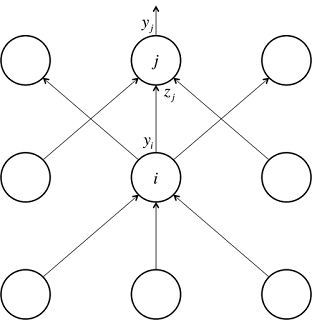
Cada unitat oculta pot afectar moltes unitats de sortida. Per tant, s'haurien de combinar molts efectes separats sobre l'error d'una manera informativa. La nostra serà una estratègia de programació dinàmica. Un cop es tinguin els derivats d'error per una capa d'unitats ocultes, seran utilitzades per calcular els derivats d'error per a les activitats de la capa següent. I una vegada que es trobin els derivats d'error per a les activitats de les unitats ocultes, és molt fàcil obtenir els derivats d'error dels pesos que condueixen a una unitat oculta. Es tornarà a definir una notació per facilitar la discussió i es fa referència al següent diagrama:
El subíndex que s'utilitza es referirà a la capa de la neurona. El símbol y es referirà a l'activitat d'una neurona, com de costum. De la mateixa manera, el símbol z es referirà al logit d'una neurona. Comencem donant una ullada al cas bàsic del problema de programació dinàmica, els derivats de la funció d'error a la capa de sortida:
Ara cal abordar el pas inductiu. Suposant que es tenen els derivats d'error per a la capa j. Ara es te la intenció de calcular els derivats d'error per a la capa que hi ha a sota, capa i. Per fer-ho, cal acumular informació sobre com la producció d'una neurona en la capa I afecta els logits de cada neurona en la capa j. Això es pot fer de la següent manera, utilitzant el fet que la derivada parcial del logit respecte a les dades de sortida entrants de la capa inferior no és més que el pes de la connexió w ij:
Ara es pot utilitzar el següent per completar el pas inductiu:
Combinant aquests dos conjunts, finalment es poden expressar els derivats parcials de la capa i en termes de les derivades parcials de la capa j. A continuació, una vegada que s'hagi passat tota la rutina de programació dinàmica, havent omplert la taula adequadament amb totes les derivades parcials (de la funció d'error respecte a les activitats de la unitat oculta), llavors es pot determinar com canvia l'error respecte als pesos.
Això dona com modificar els pesos després de cada exemple d'entrenament:
Per fer la preparació de la preparació d'una combinació d'exemples d'entrenament, només es resumeixen les derivades parcials sobre tots els exemples de formació del lot. Això dóna la següent fórmula de modificació:
S'ha aconseguit obtenir l'algoritme de backpropagation per a una xarxa neuronal avançada que utilitza neurones sigmoïdals.
El problema de l'excessiu
Ara, volem tractar d'entrenar una xarxa neuronal per identificar objectes en una imatge. Sabent que aquest és un problema complicat perquè cal utilitzar una gran xarxa neuronal (diguem-ne 20 capes) i tenim 1.000 exemples de formació. Entrenar la xarxa neuronal utilitzant l'algoritme que es descriurà, però hi ha alguna cosa que és clarament incorrecte. La xarxa neural funciona pràcticament a la perfecció en els exemples d'entrenament, però quan es passa a la pràctica, es comporta molt malament. Que està passant aquí?
El problema que s'ha detectat es diu excessiu, i això passa quan hi ha massa paràmetres al model i no hi ha prou dades d'entrenament. Per visualitzar-ho, tenint en compte la figura següent, es vol adaptar a un model als punts de dades:
Quina corba cal escollir? La línia que pràcticament no té cap exemple d'entrenament exactament? O la complicada corba que toca cada punt del conjunt de formació? Probablement caldria confiar en l'ajustament lineal en comptes de la complicada corba perquè sembla menys complicada. Aquesta situació és anàloga a la xarxa neuronal que s'ha format. Es tenen massa paràmetres, més de 100 bilions de bilions de dòlars (o 100ptilions) de paràmetres. Llavors, com evitarem l'excessiu?
Les dues maneres més senzilles són:
- Limitar les connectivitats de les neurones del model. L'arquitectura d'una bona xarxa neuronal requereix molta experiència i intuïció, i es redueix a donar llibertat al model per descobrir les relacions i, alhora, limitar-les, de manera que no se'n beneficiï.
- Afegint més exemples de formació Sovint, es pot afegir intel·ligentment i amplificar el conjunt d'entrenament existent (canviar il·luminació, aplicar canvis i altres transformacions, etc.).
Hi ha mètodes de formació més sofisticats que tracten de resoldre directament la sobreintegració, com ara la inclusió d'unes capes / neurones abandonades, però aquests mètodes estan fora de l'abast d'aquest article.
Font: KDnuggets




















Cap comentari:
Publica un comentari a l'entrada
Aquest és un blog amb moderador dels comentaris. Per tant, no apareixen immediatament